(1) 数字信号是由谐波组成的

通常而言，具有恒定循环周期的所有波形都可以分解为包括循环频率和谐波的基波，其中谐波的频率为循环频率的整数倍。[参考文献 2]基波的倍数称为谐波次数。

在准确重复波的情况下，除此之外没有任何其它频率成分。数字信号有很多循环波形。因此，在测量频率分布（称为“频谱”）时，可以准确分解为谐波，显示出离散分布的频谱。

(2) 测量时钟脉冲信号的谐波

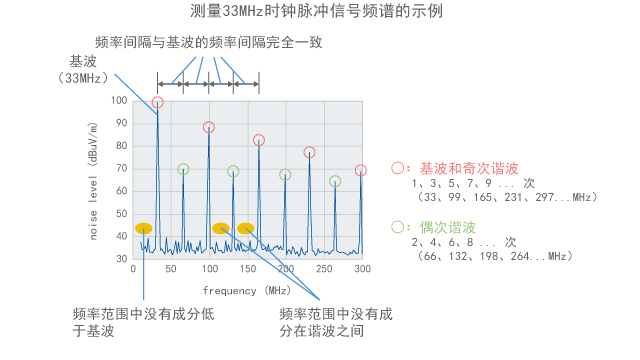
图2-4-1显示了频谱分析仪测量的33MHz时钟脉冲信号谐波的示例。像针一样向上突起的部分为谐波，其出现的间隔正好为33MHz。可以发现奇次谐波和偶次谐波的趋势不一样。最下面部分约为40dB或更低，指示频谱分析仪的背景噪声。

图2-4-1 谐波的本质

(3) 如何从噪声频率中找出噪声源

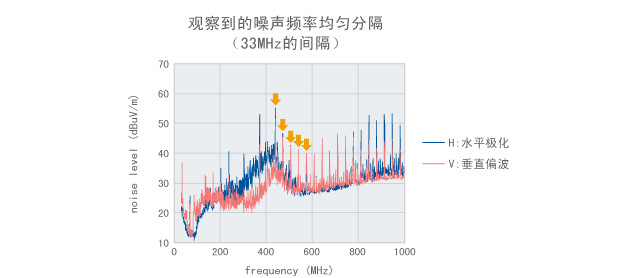
上面提及的谐波性质有助于根据噪声频率找出噪声源。通过测量噪声频谱间隔，可以类比推导出造成噪声的信号循环频率。例如，我们在电子设备中观察到了如图2-4-2所示的噪声。出现强烈噪声的频率的间隔似乎是33MHz。因此，可以认为噪声是与33MHz时钟同步运行的电路造成的。

即使此电子设备当前使用的电路具有非常接近的循环频率，如33.3MHz或34MHz，如果可以准确测量噪声频率和间隔，就可分离出这样的频率。例如，如果在图2-4-2中330MHz处存在噪声，则可以假设噪声是由33.0MHz的电路而不是33.3MHz的电路所造成的。这是因为33.3MHz或34MHz信号都不包括330MHz谐波。

(4) 只包括整数倍频率

此外，循环波形并不包括低于基频的任何频率成分。例如，100MHz信号绝不会产生20MHz、50MHz或90MHz的噪声。如果出现此种频率，则噪声是由分频信号而不是源信号所导致的。

数字电路通常与时钟脉冲信号同步运行，而且很多数字电路的运行频率为时钟脉冲信号的1/N（称为“分频”）。在这种情况下，谐波是分频信号频率的整数倍。但是，如果两个或更多电路以经过分频的相同时钟脉冲信号运行，时钟脉冲信号的谐波会与分频信号的谐波相互重叠，导致难以对其进行区分。

图2-4-2 明确显示谐波的噪声测量结果的示例